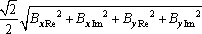B =
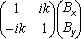 ·eiφ,
·eiφ,
where (Bx, By) are components of the magnitude vector, k - is a polarization coefficient (-1≤k≤1).
|
Properties |
Methods |
Represents a complex vector that is a pair of real vectors: one as a real part and the second as an imaginary part.
The ComplexVector represents physical quantities such as magnetic flux density, magnetic field intensity and so on for time-harmonic magnetic problems.
A pair of real vectors - one as a real part and the second as an imaginary part defines the ComplexVector.
B = BRe + i·BIm.
where the real part Bre is accessible by the Re property as Point, and an imaginary part Bim is accessible by the Im property also as Point.
Depending on the phase shift between two oscillating components of a vector, the vector can rotate clockwise or counterclockwise, or oscillate along a certain direction. Generally, the end of such a vector draws an ellipse. The semi-major axis of the ellipse corresponds to the peak value of the vector. The ratio between minor and major axes of the ellipse defines the coefficient of polarization. The coefficient of polarization is assumed to be positive for the counterclockwise and negative for the clockwise rotation. A zero coefficient corresponds to the linear polarization.
The above geometric consideration leads to the canonical form of the complex vector:
B = 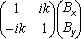 ·eiφ,
·eiφ,
where (Bx, By) are components of the magnitude vector, k - is a polarization coefficient (-1≤k≤1).
The magnitude vector is calculated by the Magnitude property as Point, phase value φ returned by the Phi and polarization coefficient is returned by the Polarization property.
You can also calculate the momentary value of a vector by given phase by Momentary property as Point and the effective (root mean square) value by the RMS as Double.
The effective value of a complex vector is calculated as:
BRMS =